변환(Transform)은 굉장히 중요합니다.
객체, 빛, 카메라를 배치, reshape(모양 재배치), 애니메이션을 다룰 수 있게 해줍니다.
Linear Transform (선형 변환)
선형 변환임을 확인하기 위해서 2가지를 만족해야한다.
- 벡터 덧셈에 대한 보존성
- 스칼라 곱에 대한 보존성
아래에 간략히 설명하겠다.

f(x) = 5x로 생각해보자
첫번째 식 : 5x + 5y = 5(x + y) => 벡터 덧셈에 대한 보존성 O
두번째 식 : k * (5x) = 5 * (kx) => 스칼라 곱에 대한 보존성 O
이렇게 만족하면 된다.
Linear Transform 의 종류로
- Scaling Transform
- Rotation Transform (원점에서의 회전)
Translaion Transform
이 있다.
Not Linear Transform (비선형 변환)
f(x) = x + (7, 3 , 2)은 비선형 변환이다.
위의 예을 사용해보자
선형은 이를 만족한다. f(x) + f(y) = f(x + y) => 5x + 5y = 5(x + y)
f(x) = x + (7, 3 , 2)를 대입하면 만족하나?
(7, 3, 2) 가 두번 더해지기 때문에 만족하지 못한다!!
그렇기 때문에
- Translaion Transform는 선형 변환이 아니다.
선형 변환과 이동(비선형 변환)을 같이하는 것은 어려울 것이다.
이를 위해 Affine Transform(아핀 변환)이 등장한다.
Affine Transform(아핀 변환)
아핀 변환은 선형 변환과 평행 이동을 함께 수행할 수 있다. ( 하지만 순서는 지켜진다. 나중되면 어떤 행렬을 먼저 곱하는 지가 중요해진다)
아핀 변환의 주요 특징은 parallelism of lines(평행성 보존) 길이 각도는 보장하지 않는다는 것이다. (변환 전에 평행했다면 변환 후에도 평행한다.)
이동, 회전, 크기, 반사, shearing 행렬 모두 Affine이다. (아핀 변환을 하기 전에 평행하던 선들은 아핀 변환 후에도 평행하다.)
Affinr Transform은 4x4 행렬로 표현하며,
이 좌표를 Homogeneous Coordinates(호모지니어스 좌표) 라고한다.
호모지니어스 좌표는 방향 벡터와 점을 같은 방식으로 나타낼 수 있게 해주며,
방향 벡터는 (vx, vy, vz, 0)으로, 점은 (vx, vy, vz, 1)로 표현됩니다.
그 이유를 먼저 설명한다면
(테블릿을 두고 와서 그림판으로 했습니다..ㅎ..ㅎ.)

빨간 원 부분이 Translation 값이 있는 곳이다.
그 부분과 곱해지는 곳이 w이다.
근데 벡터에는 Translation이라는 것이 존재하지 않는다. -> 2차원 좌표에서 v = (1,2) 가 있을 때 벡터 v가 어느 좌표에 있던 같다는 말이다. 이동은 벡터을 결정하는데 필요한 요소가 아니다.
정리
- 벡터는 방향과 길이가 같으면 같은 벡터이다. 그렇기 때문에 w가 0일 때가 벡터이다
- 점은 방향과 길이가 같고 + 위치도 같아야 한다. 그렇기 때문에 w가 1일 때가 점(point)이다
아핀 변환을 종류에 대해서 알아보자
1. Translation (이동)
Homogeneous Coordinates에서의 vector와 point를 설명할 때 잠시 말했지만,
이것이 Translation Matrix이다
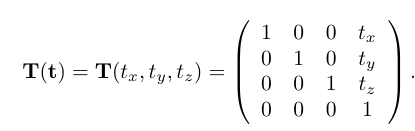
point p1이 있을 때
p1 = (px ,py , pz, 1)를 Translation Matrix과 곱하게 되면
p1' = (px + tx, py+ ty, pz + tz, 1) 이 된다.
vector p2가 있을 때
p2 = (px ,py , pz, 0)를 Translation Matrix과 곱하게 되면
p2' = (px, py, pz, 0) 이 된다.

2. Rotation (회전)
회전은 주어진 축과 각도 만큼 회전하는 것이다. 근데 원점을 기준으로!
그리고 rigid-body transform이고 handeness 이다. 라고 설명하는데
rigid body => 점간의 거리를 보존한다.
handeness => 오른손 좌표계(right-handed)인지 왼손 좌표계(left-handed)가 바뀌지 않는다.
(예를 들어, 180도 회전이든 다른 각도의 회전이든, 회전은 단순히 객체의 방향을 바꾸지만, 좌표계 자체가 반전되지는 않습니다.)
이 두가지에 유용하다.
- 위치
- 오브젝트의 방향
- 카메라 뷰 or 오브젝트의 방향
- 카메라 뷰 or 오브젝트의 방향
2차원에서의 회전을 먼저보면 3차원 회전에 대한 이해가 쉽다.
회전 전태

그리고 파이 만큼 회전하다고 하면

이렇게 된다.
2차원 회전은 이렇게 유도가 되고
3차원 회전은 이렇게 된다.

Rotation을 설명할 때 제일 첫번 째 줄에서 원점에서 회전해야 된다고 말하였다.
그 예시를 아래의 그림에서 보여준다.

만약 원점으로 이동하지 않고 회전한다면

이렇게 회전된다.
주의하도록 하자!
3. Scaling (크기)
이 행렬이 Scale Matrix이다.
Sx, Sy, Sz 는 각각의 축 방향으로 크키를 확대 및 축소한다.
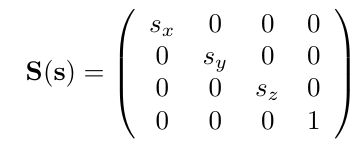
5배 커진 것을 표현할 때 아래와 같이 2가지 방법을 쓸 수 있다.

하지만 homogeneous 좌표계에서는 w(3,3)를 1로 만들어주는 과정을 거친다. 2번 째 방법을 사용하면 곱셉 or 나눗셈을 한 번 더 해줘야하기 때문에 비효율적이다. 때문에 1번을 주로 사용한다.
- Uniform Scaling: Sx = Sy = Sz 일 때
- NonUniform Scaling: Uniform Scaling이 아닐 때
역함수

사실 당연하다. X배 했으니 그것의 역은 1/X배 일 것이다.
Reflection Matrix (반사행렬, mirror matrix)
반사 행렬: Scaling Matrix에서 1개 또는 3개 (홀수 개) 의 components가 음수이다. 2개가 음수일 때는 pi radian만큼(180도) 회전한다
(여기서 설명할 때는 -1, 1을 기준으로 설명한 것이다)
아래 그림이 그 예시이다.

반사행렬을 사용할 때 주의해야 될 점이 있다.
컴퓨터가 스크린에 3D 오브젝트를 그릴 때 생각해보자.
3D 오브젝트의 전면을 보고 있을 때 뒷면을 우리가 볼 수 있을까? 없다.
그럼 그릴 필요가 있을까? 없다.
컴퓨터는 뒷면, 잘린부분, 안보이는 부분을 최대한 잘라서 안그린다.
근데 반사행렬을 잘 못쓰면 앞면을 뒷면으로 컴퓨터가 해석해서 그리지 않을 확률이있다. 그렇기 때문에 조심해야된다.
이해가 안되면 아래 글도 읽어보자..
왼손 좌표계를 쓸 때 화면을 보면
전면을 볼 때 z방향이(엄지가) 우리를 향하고 있다.
우리가 후면에 있다고 상상하고 왼손 좌표계를 해보자. 그럼 엄지는 전면을 볼 때와 반대방향으로 향하고 있다.
컴퓨터는 이렇게 엄지방향이 어디인지를 확인하면서 전면 후면을 판단한다.
Scaling In a Certain Direction (특정 방향으로 scaling)
기본적인 scaling
x,y,z 축에 대해 이루어진다.
하지만 다른 방향(여러 변형이 합쳐진)으로 하고 싶다면 어떻게 할 수 있을까?
x,y,z 축을 원하는 방 향으로 바꿔주는 것이다.
F는 축을 변환해주는 Matrix이다.

축 바꾸기 -> scaling 하기 -> 축 복구하기 이다.

'ComputerGraphics > 책' 카테고리의 다른 글
| [RealTimeRendering-4th] Transforms (3) (0) | 2024.10.18 |
|---|---|
| [RealTimeRendering-4th] Transforms (2) (0) | 2024.10.18 |
| [CUDA기반 GPU병렬 처리 프로그래밍] 벡터 합 연산 (0) | 2024.10.17 |
| [CUDA기반 GPU 병렬 처리 프로그래밍] GPGPU 및 병렬 처리 개요 (0) | 2024.09.30 |
| [RealTimeRendering-4th] The Graphics Rendering Pipeline (0) | 2024.09.09 |



