[논문정리] Stable Fluid

밀도와 온도가 거의 일정한 유체는 속도장(velocity filed)u와 압력장 p로 묘사된다.

초기 시간 t=0에서 속도와 압력이 주어졌을 때,  변수의 시간에 따른 변화는 Navier-Stokes 방정식에 의해 결정된다.

 

ν는 유체의 운동 점성계수, ρ 는 밀도, f는 외력을 의미한다.

 

Navier-Stokes 방정식은 질량(1번식) , 운동량이 보존(2번식)된다는 가정하에 성립된다.

 

이 식은 또한 경계조건을 추가해야 됩니다. ( boundary condition )

여기서는 periodic, fixed 2가지 방법을 설명합니다.

 

periodic: 벽이 존재하기 않고, 좌측 벽으로 들어가면 우측 벽에서 나온다 ( wrapping 방법 ) 

fast Fourier transform 방법으로 우아하게 구현할 수 있다.

 

fixed: 벽을 뚫고 지나갈 수 없다. 벽 방향으로 나가는 속도(normal component of velocity field)는 0이여아한다. 

 

Navier-Stokes에 등장하는 압려과 속도장은 서로 연관이 되어있습니다. 

속도에 대한 single 방정식은 1번 식과 2번 식을 결합해서 얻을 수 있고, 이것이 핵심입니다. 

 

 

아래의 방법을 보시죠

Chorin과 Marsden의 접근 방법을 따를 것입니다.

Helmholtz-Hodge Decomposition에 따르면 임의의 벡터장 w는 다음과 같이 고유하게 분해된다.

 

여기서 u는 발산이 0인 벡터장이고, q는 스칼라 field(편미분을 했으니 gradient이다) 이다. 

 

divergence free field: u (발산이 0이니, 새로 생기거나 없이지지 않으니, mass conserving이다.) 

gradient field: ∇q ( scalar field 를 미분했으니 gradient field가 된다 ) 

 

u는 주어진 유체의 회전이나 흐름을 유지하면서 질량 보존을 만족하는 성분

∇q 는 어떤 스칼라 함수 q의 그래디언트(gradient) 이므로, 특정 방향으로 유체를 밀어주는 역할을 한다.

아래의 그림은 gameDeveloper를 위한 논문에 나온 그림이다. 

 

 

 

Navier-stocks 방정식을 풀 때, 비압축성 필드(u, mass conserving, divergence free)만 필요할 때가 있다.

 

P를 any filed를 divergence free field로 만들어준다고 가정을 하면 아래와 같은 식이 성립한다.

 

그리고 3번 식의 양변에 ∇를 취해주면, 4번식을 얻을 수 있다. ( ∇ u = 0 )

 

 

4번 식은 푸아송 방정식(Poisson Equation)의 형태이다.
즉, 주어진 속도장 w의 발산을 이용해 q를 찾을 수 있습다. 

 

위해서 구한 q를 이용하면 속도장의 발산을 제거할 수 있습니다. (= vector filed에서 발산이 없는 부분만 남길 수 있다.)

아래의 식처럼 -∇q를 해주는게 곧 P를 곱해주는 것 입니다.

 

 

 

 Navier-Stoke식(2번 식)에도 P를 취해준다.

 

P는 divergence free를 만드는 것이니,

Pu = u이고(이미 divergence free), 

P * ∇p = 0이다.( P는 divergence free 요소만 남기는 것인데, 밀도의 변화는 divergence free가 아니다. 그러니  P *∇p = 0이다.)

 

위식에 P를 곱해보면 ∇p가 사라진 아래의 식이 나온다.

 

이게 나중에 stable fluid solver에서 중요하게 사용될 것이다.

시뮬레이션은 한 번 시뮬레이션할 때 4번의 time step을 거친다 .(w0->w1->w2->w3->w4)

이 그림의 의미는 w0과 w4에서는 ∇u = 0 (divergen free)여야 한다는 것이다. 

 

Method of Solution 

 

5번식의 해는 아래와 같이 4개의 단계로 이뤄진다.

 

5번 식의 오른 쪽 항을 순차적으로 계산한 후에, 마지막으로 projection (divergence free로 투영) 을 해주는 것이다. 

 

1. Add Force

외력이 크게 변하지 않으면 간단하게 외력(f)을 추가하면 된다. 

 

2. Advection

유체가 자기 자신을 어떻게 이동시키는지를 결정하는 과정이다. 비선형 항을 포함하는 요소이다. 

 

advection은 아래의 항이다.

 

이 부분을 유한차분법을 이용해서 해석한다면 time step이 충분히 작을 때만 안정적이다. 

 

우리의 논문에서는 무조건 안정적인 ( unconditionally stable ) 솔버를 제안한다. 

우리는 Method of Characteristics으로 알려져있는 편미분기반으로 구현하였다. 

 

시간 −Δt 이전의 위치로 거슬러 올라가 그 위치에서의 속도를 가져오는 방식

 

이렇게 했을 때 새로운 position에서의 속도가 이전 위체에서의 속도를 넘지 못하기 때문에 어떤 조건에서든지 안정적이다.

 

아래의 코드처럼 뒤로 가서 값을 가져온다.

def Advect_D():
    dt0 = dt * N[0]
    for i, j in ti.ndrange((1, N[0] + 1), (1, N[1] + 1)):
        pos = ti.Vector([i - U0[i, j].x * dt0, j - U0[i, j].y * dt0])

3. diffuse

viscosity를 해결하는 것이 diffuse 방정식을 해결하는 것이다. 

 

Viscosity

 

viscosity는 속도를 부드럽게 확산시키는 diffusion효과를 줍니다. 이를 구현하는 방법으로 2가지 방법이 있습니다.

 

1) Explicit

간단한 방법은 아래의 방정식을 푸는 것이다. 하지만 이렇게 명시적인 방법(explicit)으로 풀면 시뮬레이션이 불안정해집니다.

 

2) Implicit

그래서 우리는 암시적인 방법(implicit)으로 viscosity를 계산할 것이다.

논문에서 말하는 식은 다음과 같은데 왜 이렇게 된건지 공책에 끄적여봤다.

 

Implicit은 미래에(1 time step앞에) 값에 변경되는 값을 되돌려서 현재의 값을 구하는 방법이다. 

그래서 미래의 속도에서 미래의 점성을  빼준 식을 정리하면 논문에 말하는 식이 된다.

 

 

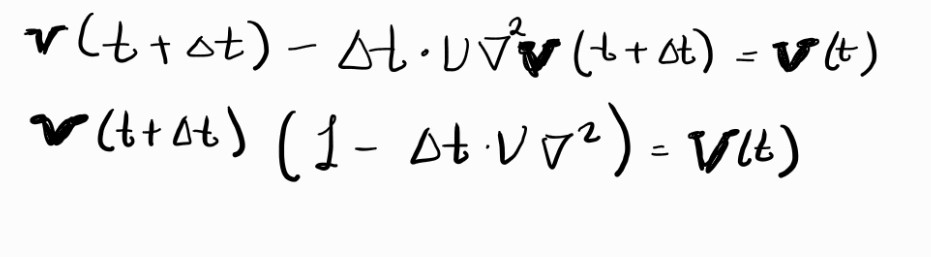
4. Projection Step

 

이 과정은 결과 field를 발산이 0인 (divergence free) field로 만들어준다.

이 단계에서는 Poisson 방정식을 해결해야 하며, 4번 식과 같이 정의된다. 

q를 이용해서 다음과 같이 속도장을 보정한다.

 ( - ∇ q 하는 것이, divergence free field만 남겨주는 것 )  

 

 

 

 

 

Periodic Boundaries and the FFT

 

Our Solver

NDIM: 차원

O[NDIM]: 원점

L[NDIM]: 축의 길이

D[NDIM]: grid 한칸 길이 (L[i] / N[i])

 

그리고 유속은 cell의 중심에 정의할 것이다. 

 

우리는 속도를 위한 2개의 U0, U1 grid를 만들 것이다.  이전 스텝의 속도는 U0에 새로운 속도는 U1에 따로 저장해두고 값을 swap해서 최신화할 것이다. 

 

물리량에 대한 정보는 S0,S1에 저장한다. time step은 dt로 저장한다. (우리 시물레이션은 dt가 켜져도 안정적인 시뮬레이션이 가능하다) 

 

점성은 v, diffusion 상수는 ks, 소산률은 as로 저장한다. 

경계조건은 periodic이나  fixed 중에서 선택해서 사용히면 된다. 

 

이제 시작해보자

직접 구현을 해보니 이 논문이 더 도움이 될 것 같습니다.

저도 이 논문을 보면서 구현했고, 구현 링크도 올리겠습니다. 

https://tithingbygame.tistory.com/155

[논문정리] Real-Time Fluid Dynamics for Games

https://github.com/GameTithe/stable_fluid_taichi