구현한 코드이다
https://github.com/GameTithe/SPH-Vpython
Claude Navier 와 George Stokes가 유체역학을 설명하는 Navier-Stokes 방정식을 공식화 하였다.
운동량 보존을 설명하기 위한 Navier-Stokes외에도
질량을 보존하는 연속 방정식(continuity equation)과 에너지 보존을 설명하는 상태 방정식(state equation)이 추가적으로 필요하다.
Paticle based는 Lagrancian approach(랑그랑주 접근법), Grid based는 Eulerian approach(오일러 접근법)으로 유체 시뮬레이션에 사용되었다.
여기서는 Particle 기반 접근법인 SPH(Smoothed Particle Hydrodynamics)에 대해 설명합니다.
Smoothed Particle Hydrodynamics
SPH는 Particle system을 위한 보간 방법이다. SPH를 사용하면 입자 위치에서 정의된 quantity field를 어느 공간에서든지 평가가 가능하다.
SPH는 이웃간의 물리량을 smoothing kernel을 사용해서 보간한다.
아래의 식은 SPH에서의 물리량 A를 나타내는 식이다.
m: 질량
r: 위치
p: 밀도
A: r에서의 물리량
W: smoothing Kernel (2차 정확도인)

또한 위의 식을 미분했을 때는 kernel만 영향을 받는다. ( 다른 부분은 상수이기에..)
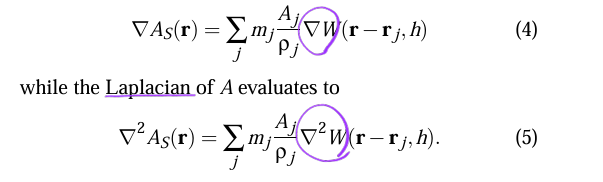
밀도
위의 식을 이용해서 밀도를 구해보자.

SPH에는 몇가지 문제가 존재한다.
힘의 대칭성(symmetry of force)과 운동량 보존(conservation of momentum) 같은 원리를 보장하지 않는다. 이를 해결하기 위한 방법을 아래에서 알아보자
Modelling Fluids with Particles
Eulerian approach(오일러 접근법, grid based)에서 isotheram fluid는 속도, 밀도, 압력 3가지 field로 정의된다.
시간에 따른 물리량의 변화는 2가지 식으로 평가할 수 있다.
첫번째 식은 질량 보존 법칙을 보장하고
두번째 식(Navier-Stokes Equation)은 운동량 법칙을 보장한다.


Particle Based Approach를 한다면 식이 단순해질 수 있다.
우선 질량 보존 방정식을 생략할 수 있다.
시뮬레이션할 때 입자 개수가 동일하고, 질량은 계속해서 동일하기 때문에 질량 보존 법칙이 자동으로 성립한다.
두번 째
우측식에서
우측 방정식에서 우변에는 세 개의 힘 밀도(force density) 필드가 존재한ㄷ.
압력력(Pressure force): −∇p
외력(External force): ρg
점성력(Viscous force): μ∇2v
이 세 가지 힘 밀도 항들의 합은 다음과 같이 표현할 수 있다.

그리고 왼쪽식을 보면 속도를 시간으로 미분한 부분을 a(가속도)로 볼 수 있다.
정리하면 오른쪽 식이 된다.


압력
불행하게도 이 힘은 대칭적이지 않다.
예를 들어서 보면 입자i의 kernel의 gradient는 중심에서 0이다. 그럼 i의 입자는 j의 입자의 압력만을 사용하게 된다.
아래와 같이 식을 살짝 바꿔주면 ( => ( pi + pj) / 2 ) 간단히 해결할 수 있다.

점성
이 힘 또한 비대칭적이다. 점성은 입자마다 다양하게 존재한다. 점성력은 속도차이에 의존하기 때문에 이를 사용하면 자연스럽게 해결할 수 있다.

외부 힘
벽에 부딫히거나,중력 등과 같은 간단한 힘은 입자에 직접 적용하면 된다.
Smoothing Kernel
안정성, 정확성, 속도를 위해서 Smoothing Kernel을 선택하는 것은 중요하다.
입자의 boundary( 바깥쪽 ) 의 도함수가 0이면 안정적이다.
여기서는 3가지 Kernel을 소개한다.
왼쪽부터 순서대로, poly6, spiky, viscosity 이다.

두꺼운 부분인 Kernel값, 얇은 부분이 gradient, 점선이 Laplacian 값이다.



ploy6은 gradient가 입자 중심에서는 0이다. 그렇게 될 경우 압력이 높을 때 입자 중심에서 밀어내는 힘을 주지 못하기 때문에 군집현상이 일어날 수 있다.
그래서 spiky kernel을 사용하는게 바람직하다.
점성을 계산할 때 viscosity kernel 는 라플라시안이 양수이기에 안정적이다.
'ComputerGraphics > 논문 정리' 카테고리의 다른 글
| [논문정리] Taichi: A Language for High-Performance Computation on Spatially Sparse Data Structures (0) | 2025.03.12 |
|---|---|
| [논문정리] MPM Course (0) | 2025.03.06 |
| [논문정리] Real-Time Fluid Dynamics for Games (0) | 2025.02.18 |
| [논문 정리] Gaussian Ray Tracing: Fast Tracing of Particle Scenes (ing) (0) | 2024.11.14 |
| [논문저장소] Gaussian Splatting (미완..이여서 미안...해서 실행시키는 법을 곁들였습니다) (0) | 2024.11.10 |



