https://raytracing.github.io/books/RayTracingInOneWeekend.html
https://raytracing.github.io/books/RayTracingInOneWeekend.html
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ [Listing [assume-rtw-vec3]: [vec3.h] Assume rtweekend.h inclusion for vec3.h] And now the new main: ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
raytracing.github.io
레이트레이싱의 바이블 in one weekend를 보면서 공부한 내용을 정리해봤습니다.
구를 그린 후 부터 정리했습니다. 모든 코드는 사이트에 잘 정리해졌기에 핵심 내용들을 간략히 정리했습니다.

anti-aliasing


1번 이미지가 pixel 1개에 ray를 한 번 쏴서 색을 구한 것이다.
2번 이미지는 pixel주변에 ray를 100번 쏴서 평균 값으로 색을 구한 것이다.
1번 이미지와 같이 계단식 aliasing을 없애기 위해서는 주변 pixel들의 색을 적절히 섞어줘야 된다.
아래 그림과 같이 sample square(주변 pixel)에서 색을 가져오고 평균을 내서, 색을 결정한다.

ray get_ray(int i, int j)
{
vec3 offset = sample_square();
vec3 pixel_sample = pixel00_loc + ( (offset.x() + i) * pixel_delta_u) +
( (offset.y() + j) * pixel_delta_v);
auto ray_origin = center;
vec3 dir = pixel_sample - center;
return ray(ray_origin, dir);
}Diffuse Material
Diffuse는 난반사이다.
아래의 그림처럼, 3개의 ray를 쐈을 때, 방향이 같은 ray라고 해서, 동일한 방향으로 반사 되는 것이 아니라,
랜덤한 방향으로 반사가 된다.

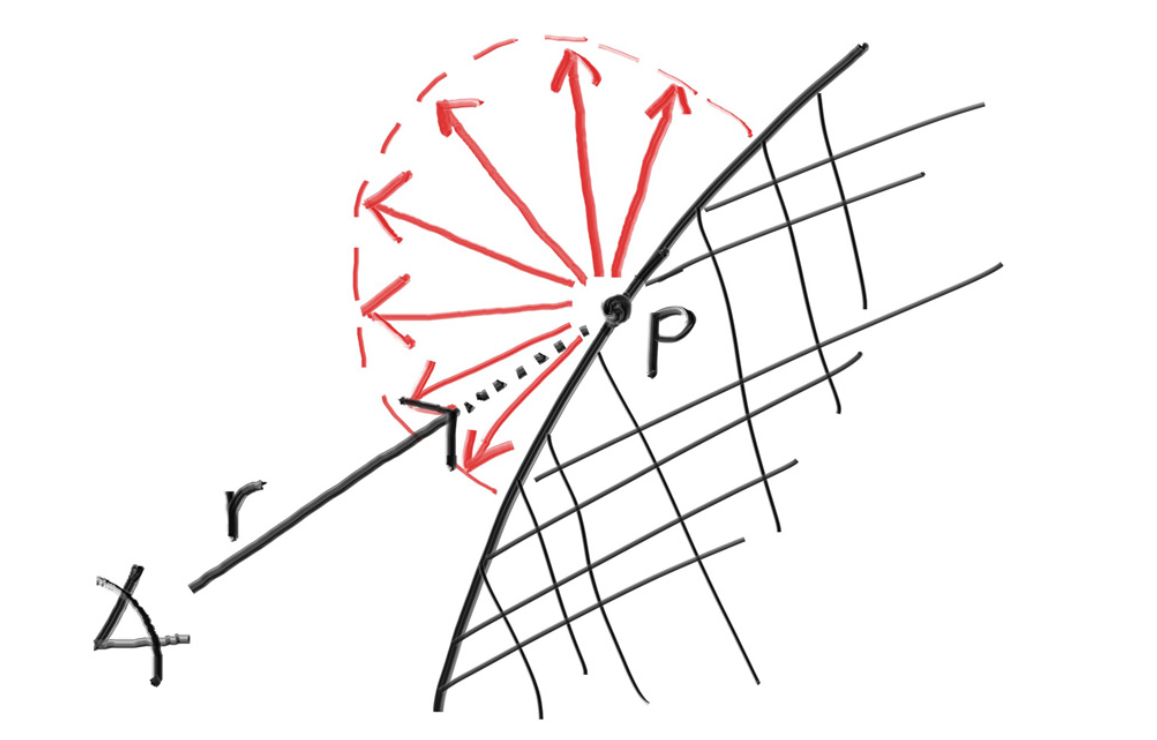
우리는 랜덤으로 반사되는 방법을 사용할 것인데, 랜덤으로 반사가 되도록 하면 흡수가 되는 경우( 반사가 구 안쪽으로)가 생긴다.
이런 상황은 만들어주기 싫기에, 반원만 사용할 수 있도록 함수를 만든다.
dot product를 사용해주면, normal vector와 랜덤으로 만들어진 벡터간의 방향 차를 알 수 있다.
inline vec3 random_on_hemisphere(const vec3& normal)
{
vec3 on_unit_sphere = random_unit_vector();
if (dot(normal, on_unit_sphere) > 0)
{
return on_unit_sphere;
}
else
{
return -on_unit_sphere;
}
}

난반사까지 만들어줬다면, 색을 구할 때 난반사를 활용한다.
object에 부딫혔을 때, 난반사를 만들어주고,
만들어진 난반사 surface에서 다시 ray를 만들어서 쏴준다.
만약
object에 또 부딫혔을 때, 난반사를 만들어주고,
만들어진 난반사 surface에서 다시 ray를 만들어서 쏴준다.
만약
object에 또 부딫혔을 때, 난반사를 만들어주고,
만들어진 난반사 surface에서 다시 ray를 만들어서 쏴준다.
만약
object에 또 부딫혔을 때, 난반사를 만들어주고,
만들어진 난반사 surface에서 다시 ray를 만들어서 쏴준다.
....
이렇게 반복을 하다가, 정해진 횟수 만큼 반사가 되었거나, 더 이상 object에 부딫히지 않았을 때 종료한다.
그럼 아래와 같이 결과를 얻을 수 있다.
(depth는 반사 횟수를 위해 추가했다.)
color ray_color(const ray& r, int depth, const hittable& world)
{
hit_record rec;
if (depth <= 0) return color(0, 0, 0);
if (world.hit(r, interval(0, infinity), rec))
{
//return 0.5 * (rec.normal + color(1, 1, 1));
vec3 direction = random_on_hemisphere(rec.normal);
return 0.8 * ray_color(ray(rec.p, direction), depth - 1, world);
}
// background color
vec3 unit_direction = unit_vector(r.direction());
auto a = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - a) * color(1.0, 1.0, 1.0) + a * color(0.5, 0.7, 1.0);
}
ShaderAcen
float의 정확성에는 한계가 존재한다. 그렇기 때문에 충돌감지를 할 때 잘 못된 정보를 반환할 수 있다.
만약 0.000000001 정도의 차이로 구, 면, 바닥, 등 오브젝트 위에 존재하는데, 안에 있다고 인식할 수도 있다.
(그럴 경우 반사가 제한되는 경우가 생긴다. 그래서 이를 우회해주면 조금 더 밝게 보인다)
그래서 우리는 0.01정도 차를 줘서 우회해보자.
color ray_color(const ray& r, int depth, const hittable& world)
{
hit_record rec;
if (depth <= 0) return color(0, 0, 0);
//if (world.hit(r, interval(0, infinity), rec))
if (world.hit(r, interval(0.001, infinity), rec))
{
vec3 direction = random_on_hemisphere(rec.normal);
return 0.5 * ray_color(ray(rec.p, direction), depth - 1, world);
}
// background color
vec3 unit_direction = unit_vector(r.direction());
auto a = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - a) * color(1.0, 1.0, 1.0) + a * color(0.5, 0.7, 1.0);
}


True Lambertian Reflection
우리가 위에서 한 것과 같이, 반구를 사용한 Diffuse 표현도 있지만, 조금 더 사실적으로 표현 가능한 방법으로는 Lambertian 방법이 있다.
Lambertian 분포는 normal vector 쪽으로 반사되는 양이 많고, normal vector에서 멀어질 수록 더 적게 반사되는 것을 고려한 방법이다.
이를 구현하기 위해서 ramdom unit vector를 사용한다. ( 0~1 범위의 vector를 랜덤으로 가져오는... 최대 1범위로 랜덤하게 뽑으니 자연스럽게 구 모양)

빛과 접한 point + unit normal vector 를 해준 곳에서 random unit vector를 구한다.
color ray_color(const ray& r, int depth, const hittable& world)
{
hit_record rec;
if (depth <= 0) return color(0, 0, 0);
if (world.hit(r, interval(0.001, infinity), rec))
{
//vec3 direction = random_on_hemisphere(rec.normal);
vec3 direction = rec.p + unit_vector(rec.normal) + random_unit_vector();
return 0.5 * ray_color(ray(rec.p, direction), depth - 1, world);
}
// background color
vec3 unit_direction = unit_vector(r.direction());
auto a = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - a) * color(1.0, 1.0, 1.0) + a * color(0.5, 0.7, 1.0);
}
변화된 것은
1. 그림자가 뚜렸해졌다.
normal vector쪽으로 빛이 많이 나가니 그림자가 뚜렸해졌다.
(하단에서의 normal로 가니 계속 바닥이 부딪힐 것이고, 중단, 중하단에서도 그림자를 적게 만들어 줄 것이다.)
2. 조금 더 어두워졌다.
더 많은 광선이 전체적으로 뭉쳐서 난반사된고, 카메라가 그 구역에 해당되지 않으면 결과적으로 어두워 보이는 현상이 발생한다.
Gamma Correction
Gamma Correction이란 색을 조정을 해주는 것인데,
인간은 어두운 색상 정보에 더 민감하고, 밝은 것에는 둔하다.
그래서 이미지를 조금 더 밝게 저장해야지 우리가 생각한 것과 같은 색으로 인식을 하다는 것이다.
일반적으로는 2.2 제곱을 한다.
저장할 때에는 1 / 2.2 제곱을 해서 더 밝게 저장한다. ( 0.xx이니 1/2.2 제곱을 해야 수치가 커진다. )
그리고 수치를 바꿀 일이 있다면 2.2 제곱을 하고 수치를 조정해줘야된다.
이와 같은 원리로 우리가 지금까지 출력한 구도 우리가 예상한 색을 입혀주기 위해서는 gamma correction을 적용해줘야 된다. 1 /2.2 제곱은 sqrt 로 대체할 수 있다. 1 / 2나 1 /2.2나 비슷하니까..
inline double linear_to_gamma(double linear_component)
{
if (linear_component > 0)
return std::sqrt(linear_component);
return 0;
}
void write_color(std::ostream& out, const color& pixel_color) {
auto r = pixel_color.x();
auto g = pixel_color.y();
auto b = pixel_color.z();
// Apply a linear to gamma transform for gamma 2
r = linear_to_gamma(r);
g = linear_to_gamma(g);
b = linear_to_gamma(b);
static const interval intensity(0.000, 0.999);
int rbyte = int(256 * intensity.clamp(r));
int gbyte = int(256 * intensity.clamp(g));
int bbyte = int(256 * intensity.clamp(b));
// Write out the pixel color components.
out << rbyte << ' ' << gbyte << ' ' << bbyte << '\n';
}
확실히 밝아진 것을 알 수 있다.
좌측이 적용 전, 우측이 적용


Reflection(정반사)


Fuzzy Reflection
Fuzzy Reflection은 거칠거나 매끄럽지 않은 표면에서 빛이 반사될 때 나타나는 효과이다.
이를 구현하기 위해서는 위와 가팅 정반를 하는 것이 아니라, 반사를 랜덤하게 시켜줘야 된다.
아래 그림을 보면, 이제는 금방 어떻게 해야 될지 떠오를 것이다. lambertian과 비슷하게 처리를 해주면 바로 구현이 가능하다.
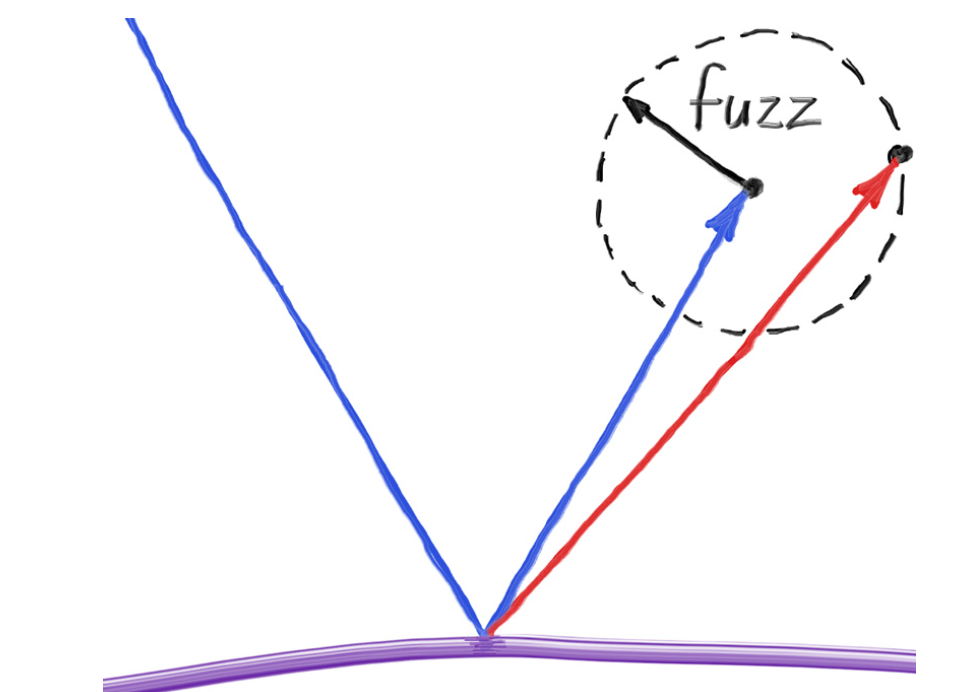
정반사를 먼저한 다음에 그 위치에서 random_unit_vector를 구해줘서 샘플링을 해오면 된다.
fuzzy 수치도 같이 곱해주면, random_unit_vector의 크기를 조절할 수 있기 때문에 fuzzy 값을 높이면 더 뿌옇게? 보이게 할 수 있다.
bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered)
const override {
vec3 reflected = reflect(r_in.direction(), unit_vector(rec.normal));
reflected += random_unit_vector() * fuzzy;
scattered = ray(rec.p, reflected);
attenuation = albedo;
return true;
}
좌측이 fuzzy parameter가 0.3, 우측이 1.0이다.

Dielectrics
지금까지 반사를 주로 다뤘지만, 빛은 반사외에도 흡수도 가능하고, 그때 빛에 굴절이 생길 수 있다.
물, 유리, 다이아몬드와 같은 투명한 재질을 유전체(dielectric)라고 한다.
빛이 유전체에 닿으면, 빛은 반사광선(reflected ray)과 굴절광선(refracted ray)으로 나뉘고, 우리는 이를 선택해서 렌더링 해야 된다.
굴절률은
물체의 굴절률 / 환경 굴절률이다.
만약 물 속에 있는 유리 구슬을 렌더링하고 싶다면, 유리구슬 굴절률 / 물 굴절률 인 것이다.
Refraction
Snell's law

η: 입사 광선이 있는 매질의 굴절률
η': 굴절 광선이 있는 매질의 굴절률
θ': 입사 광선과 표면 법선(normal) 사이의 각도
θ: 굴절 광선과 표면 법선 사이의 각도

이제 아래는 공식에 대해서 설명을 하는데, 유도 과정은 중요하지 않다고 생략을 했다.
코드고 이 공식과 똑같이 구현하면 잘 된다...!

실패했던 모습,,, normal은 꼭 normralize를 해주자! 우측은 성공


아래가 snells law이다.

만약에 , η′=1.0 일 때,
sinθ′ = 1.5 * sinθ이 된다.
sin은 최대 값이 1이다.
이때 세타가 90도라면? sinθ′ = 1.5?? 말이 안된다. 이때는 굴절에 사용하는 snell의 법칙이 유효하지 않게 되는 것이다.
(임계각이라고 하는 것으로 알고 있다)
이럴 때는 굴절이 아닌 반사가 일어난다.
임계각에 대한 영상첨부 :)
https://www.youtube.com/watch?v=NAaHPRsveJk
임계각에 대한 설정을 해주고, 그에 맞게 reflect, refract를 설정해준다.
ri 에 front face에서 역수를 취한이유는
ri에 우리는 물체 굴절률 / 환경 굴절률 을 할당했다.
front face에서는 환경에서 물체로 이동하는 것이기 때문에 사용해야 되는 값은 환경 굴절률 / 물체 굴절률이다. 그래서 front face일 때 역수를 취한 것이다.
bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered)
const override {
attenuation = color(1.0, 1.0, 1.0);
double ri = rec.front_face ? (1.0 / refraction_index) : refraction_index;
vec3 unit_direction = unit_vector(r_in.direction());
double cos_theta = dot(-unit_direction, unit_vector(rec.normal));
double sin_theta = sqrt(1 - cos_theta * cos_theta);
bool cannot_refract = ri * sin_theta > 1.0;
vec3 direction;
if (cannot_refract)
{
direction = reflect(unit_direction, unit_vector(rec.normal));
}
else
{
direction = refract(unit_direction, unit_vector(rec.normal), ri);
}
scattered = ray(rec.p, direction);
return true;
}
물체와 맞닿아 있는 부분은 굴절이 되고 있고, (구형이라서 반사처럼 보이지만.. 사실 굴절임...)
(theta가 작다 -> sin이 작다 -> 굴절이 가능하다.)
멀어지니까 반사하는 모습을 볼 수 있다. 반사는 명백히 보인다.

Schlik Approximation
Schlick Approximation은 입사각에 따른 반사율 변화를 근사적으로 계산한다.
물체에서는 반사와 굴절이 동시에 일어난다. shilck approximation을 통해 그 확률을 구하고, 확률적으로 처리를 해주는 것이다.
그리고 schlik approximation을 대략 계산해보면 굴적률이 1/1.3일 때 cos(theta)를 0.5라고 해서 0.0X 정도이다. 매우매우 작은 값이고, 90도 가까워져야지 급격히 커진다.
그래서 수직에 가까워질 수록 자연스럽게 반사처리를 도와주고, 각도가 수직과 멀어지면 거의 영향을 안준다.
if (cannot_refract || reflectance(cos_theta, ri) > random_double())
direction = reflect(unit_direction, rec.normal);
...
static double reflectance(double cosine, double refraction_index) {
// Use Schlick's approximation for reflectance.
auto r0 = (1 - refraction_index) / (1 + refraction_index);
r0 = r0*r0;
return r0 + (1-r0)*std::pow((1 - cosine),5);
}
미세하지만, 그래도 자연스러워진것... 같다... :_


비눗방울 만들기
구1: 공기 -> 물
구2: 물 -> 공기
이렇게 구 2개를 배치해주면 자연스럽게 비눗방울이 된다!

Defocus Blur
원리 먼저 봐야 이해하기가 쉬울 것이다.
핀홀 카메라(Pinhole camera)
‘작은 구멍(핀홀)’만을 통해 빛이 들어오도록 만들면 원근감은 제대로 표현되지만, 빛이 아주 적게 들어오므로 실제 카메라로는 쓰기 힘들다. (핀홀을 오래 열어두거나, 아주 어두운 이미지를 얻게 됨)
실제 카메라는 핀홀이 아님
더 많은 빛을 받기 위해, 실제 카메라는 렌즈와 큰 구멍(조리개, Aperture)을 사용해 빛을 모은다.
그런데 구멍이 커지면(조리개가 열리면) 멀리 있거나 가까이 있는 물체가 정확히 한 점으로 맺히지 않고, 초점 거리(focus distance)와 다르게 떨어진 물체들은 흐릿하게(blur) 보이게 된다.
초점 거리(focus distance)
카메라가 초점을 맞추는 ‘특정 거리’다. focual length와는 다른 의미이다. (하지만 여기서는 같은 거리에 있다으니, 같다고 가정하고 구현할 것 이다.)
그 거리에 있는 물체는 선명하게 보이고, 그보다 앞뒤로 멀어지면 점점 더 흐리게 보인다.
Defocus Blur 구현
그래픽스에서 진짜 복잡한 렌즈 구성을 그대로 구현할 필요는 없다.
시스템을 구현하는 대시 신 얇은 렌즈(Thin Lens) 모델을 사용해서
어느 정도 거리에서만 초점이 맞고, 그 앞뒤로는 흐려지는 효과를 내보자.'
blur처리가 되는 이유는 이런 느낌인 것 같다.
초점 맞춘 곳에 viewport를 만든 것이니, 다른 거리에 있는 물체들은 자연스럽게 blur가 되어버리는...
defocus_radius는 focus_dist에 맞게 만들어준다. ( focus_dist에 존재하는 물체가 focusing 될 수 있도록)
auto defocus_radius = focus_dist * std::tan(degrees_to_radians(defocus_angle / 2));
defocus_disk_u = u * defocus_radius;
defocus_disk_v = v * defocus_radius;
아래의 그림이 조금은 도움이 되길 바란다..
focus_dist에 있는 물체만이 원하는 픽셀에 원하는 색상을 넣을 수 있고, 다른 물체들은 픽셀이 어긋난다.

ray의 출발점을 랜덤으로 잡고(blur를 위해서) ray를 쏴준다.
ray get_ray(int i, int j) const {
auto offset = sample_square();
auto pixel_sample = pixel00_loc
+ ((i + offset.x()) * pixel_delta_u)
+ ((j + offset.y()) * pixel_delta_v);
auto ray_origin = (defocus_angle <= 0) ? center : defocus_disk_sample();
auto ray_direction = pixel_sample - ray_origin;
return ray(ray_origin, ray_direction);
}
...
point3 defocus_disk_sample() const {
auto p = random_in_unit_disk();
return center + (p[0] * defocus_disk_u) + (p[1] * defocus_disk_v);
}
사실 본인은 이 부분 내용이 이해가 잘 안되어서 조금 헤맸다. 여러가지 테스트를 해봤다.
defocust_dist_sample에서 random vector를 왜 사용하지라는 의문이 들었다.
안하면 안되나 어차피 거리가 알아서 픽셀 도착 지점을 바꾸니 blur가 되지 않을까 생각했지만, 그렇지 않았다.
하지만 두개의 이미지를 두고 비교해보니 차이점은 존재했다.
예상했던 대로 픽셀 도착 지점을 바꾸고는 있었다. focus에서 벗어난 물체들을 보면 크기가 다르다는 것을 볼 수 있다.
픽셀 도착 지점을 바꾸지만, 어쨋든 비율이 좋게 잘 도착을 하니, blur효과는 일어나지 않고, 크기 조정만 된것이다.


여기에 random 함수를 추가해줘야지, blur까지 해결이 가능한 것이다!
아래 그림은 random이 focus된 물체에는 영향을 안주는 이유이다.
저는 많이 헤맸지만, 이걸 읽은 분들은 잘 해결할 수 있었으면 좋겠네요


그럼 defocus_angle이 커져도 초점에 맞는 구는 영향을 받으면 안되겠죠?
defocus_angle을 키워봤습니다! 영향을 받네요! ㅎ....
코드가 잘못됐다기 보다 구는 3d이니 어쩔수 없이 모든 pixel이 같은 dist에 있을 수 없습니다.
그래서 어쩔 수 없이 초점을 맞춘 구도 blur 영향을 받네요


여기까지가 A weekend 내용의 전부입니다 고생하셨습니다
'ComputerGraphics' 카테고리의 다른 글
| [CG] Bloom Effect 구현 (0) | 2025.01.21 |
|---|---|
| [실습 저장소] Projected Texture(+alpha blending) (0) | 2025.01.21 |
| [CG] FrameBuffer 사용해서 postProcessing(후처리) (0) | 2025.01.15 |
| [CG] Multi Light + Fog Effect 구현 (0) | 2025.01.14 |
| [CG] Shadow Map using Depth Map (0) | 2024.12.08 |



